Essence of calculus

In this first video of the series, we see how unraveling the nuances of a simple geometry question can lead to integrals, derivatives, and the fundamental theorem of calculus.

Derivatives center on the idea of change in an instant, but change happens across time while an instant consists of just one moment. How does that work?

A few derivative formulas, such as the power rule and the derivative of sine, demonstrated with geometric intuition.

A visual explanation of what the chain rule and product rule are, and why they are true.

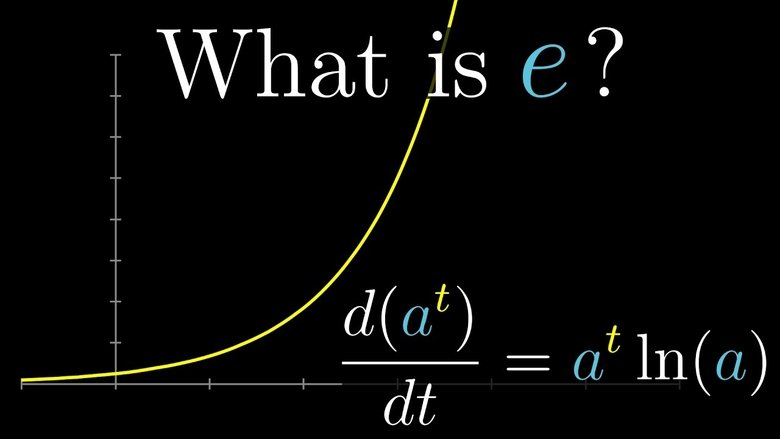
What is e? And why are exponentials proportional to their own derivatives?

Implicit differentiation can feel weird, but what's going on makes much more sense once you view each side of the equation as a two-variable function, f(x, y).

Formal derivatives, the epsilon-delta definition, and why L'Hôpital's rule works.

What is an integral? How do you think about it?

Integrals are used to find the average of a continuous variable, and this can offer a perspective on why integrals and derivatives are inverses, distinct from the one shown in the last video.

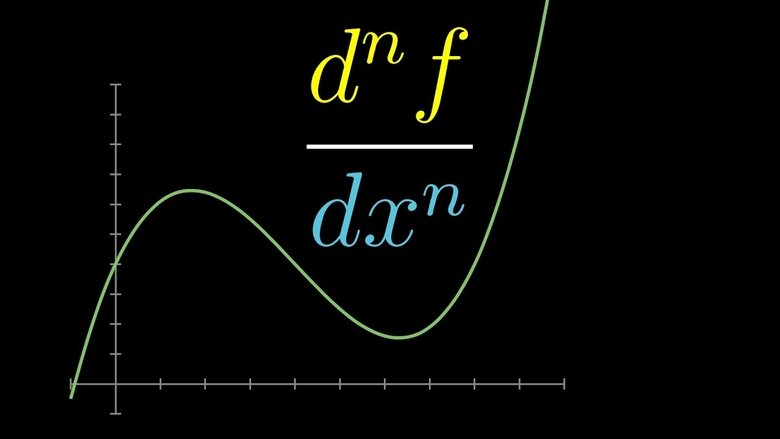
A very quick primer on the second derivative, third derivative, etc.

Taylor polynomials are incredibly powerful for approximations, and Taylor series can give new ways to express functions.

A visual for derivatives which generalizes more nicely to topics beyond calculus.